NBA Win Percentage
On ESPN if you watch the gamecast of a game they give an updated win percentage as the game progresses. We are going to produce a similar prediction, calculating win percentage for a home team given point differential, quarter, and time left in the game.
We are calculating:
p(home_win|[time_left, point_diff]=[t,p])
We’ll do the simplest frequentist prediction by counting up the number of games where [t,p] occurs and then counting up the number of games where that [t,p] occurs and the home team won. This project is mostly to practice working with data both in python, but also later in SQL because I will perform this same analysis with an NCAA BigQuery database.
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
from matplotlib import pyplot as plt
%matplotlib inline
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# Any results you write to the current directory are saved as output.
/kaggle/input/nba-playbyplay-data-20182019/NBA-PBP-2018-2019.csv
df = pd.read_csv('/kaggle/input/nba-playbyplay-data-20182019/NBA-PBP-2018-2019.csv')
df.head()
| URL | GameType | Location | Date | Time | WinningTeam | Quarter | SecLeft | AwayTeam | AwayPlay | ... | FreeThrowNum | EnterGame | LeaveGame | TurnoverPlayer | TurnoverType | TurnoverCause | TurnoverCauser | JumpballAwayPlayer | JumpballHomePlayer | JumpballPoss | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | /boxscores/201810160BOS.html | regular | TD Garden Boston Massachusetts | October 16 2018 | 8:00 PM | BOS | 1 | 720 | PHI | Jump ball: J. Embiid vs. A. Horford (B. Simmon... | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | J. Embiid - PHI | A. Horford - BOS | B. Simmons |
| 1 | /boxscores/201810160BOS.html | regular | TD Garden Boston Massachusetts | October 16 2018 | 8:00 PM | BOS | 1 | 700 | PHI | R. Covington misses 3-pt jump shot from 27 ft | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2 | /boxscores/201810160BOS.html | regular | TD Garden Boston Massachusetts | October 16 2018 | 8:00 PM | BOS | 1 | 700 | PHI | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 3 | /boxscores/201810160BOS.html | regular | TD Garden Boston Massachusetts | October 16 2018 | 8:00 PM | BOS | 1 | 675 | PHI | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 4 | /boxscores/201810160BOS.html | regular | TD Garden Boston Massachusetts | October 16 2018 | 8:00 PM | BOS | 1 | 673 | PHI | Defensive rebound by D. Saric | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
5 rows × 40 columns
df.columns
Index(['URL', 'GameType', 'Location', 'Date', 'Time', 'WinningTeam', 'Quarter',
'SecLeft', 'AwayTeam', 'AwayPlay', 'AwayScore', 'HomeTeam', 'HomePlay',
'HomeScore', 'Shooter', 'ShotType', 'ShotOutcome', 'ShotDist',
'Assister', 'Blocker', 'FoulType', 'Fouler', 'Fouled', 'Rebounder',
'ReboundType', 'ViolationPlayer', 'ViolationType', 'TimeoutTeam',
'FreeThrowShooter', 'FreeThrowOutcome', 'FreeThrowNum', 'EnterGame',
'LeaveGame', 'TurnoverPlayer', 'TurnoverType', 'TurnoverCause',
'TurnoverCauser', 'JumpballAwayPlayer', 'JumpballHomePlayer',
'JumpballPoss'],
dtype='object')
df['home_pt_diff'] = df.HomeScore - df.AwayScore
df.tail()
| URL | GameType | Location | Date | Time | WinningTeam | Quarter | SecLeft | AwayTeam | AwayPlay | ... | EnterGame | LeaveGame | TurnoverPlayer | TurnoverType | TurnoverCause | TurnoverCauser | JumpballAwayPlayer | JumpballHomePlayer | JumpballPoss | home_pt_diff | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 613666 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 4 | 0 | TOR | K. Leonard makes free throw 1 of 2 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -3 |
| 613667 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 4 | 0 | TOR | K. Leonard makes free throw 2 of 2 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -4 |
| 613668 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 4 | 0 | TOR | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -4 |
| 613669 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 4 | 0 | TOR | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -4 |
| 613670 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 5 | 0 | TOR | End of Game | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -4 |
5 rows × 41 columns
df['time_left'] = (4-df.Quarter)*720+df.SecLeft
df.tail()
| URL | GameType | Location | Date | Time | WinningTeam | Quarter | SecLeft | AwayTeam | AwayPlay | ... | LeaveGame | TurnoverPlayer | TurnoverType | TurnoverCause | TurnoverCauser | JumpballAwayPlayer | JumpballHomePlayer | JumpballPoss | home_pt_diff | time_left | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 613666 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 4 | 0 | TOR | K. Leonard makes free throw 1 of 2 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -3 | 0 |
| 613667 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 4 | 0 | TOR | K. Leonard makes free throw 2 of 2 | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -4 | 0 |
| 613668 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 4 | 0 | TOR | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -4 | 0 |
| 613669 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 4 | 0 | TOR | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -4 | 0 |
| 613670 | /boxscores/201906130GSW.html | playoff | Oracle Arena Oakland California | June 13 2019 | 9:00 PM | TOR | 5 | 0 | TOR | End of Game | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | -4 | -720 |
5 rows × 42 columns
# Only need a few of these columns to perform
df.drop(['URL', 'GameType', 'Location','AwayPlay', 'HomePlay',
'Shooter', 'ShotType', 'ShotOutcome', 'ShotDist',
'Assister', 'Blocker', 'FoulType', 'Fouler', 'Fouled', 'Rebounder',
'ReboundType', 'ViolationPlayer', 'ViolationType', 'TimeoutTeam',
'FreeThrowShooter', 'FreeThrowOutcome', 'FreeThrowNum', 'EnterGame',
'LeaveGame', 'TurnoverPlayer', 'TurnoverType', 'TurnoverCause',
'TurnoverCauser', 'JumpballAwayPlayer', 'JumpballHomePlayer',
'JumpballPoss', 'AwayScore', 'HomeScore','Quarter','SecLeft'], axis=1, inplace=True)
games_groupby = df.groupby(['Date', 'Time', 'HomeTeam', 'WinningTeam'])
games_groupby.count()
| AwayTeam | home_pt_diff | time_left | ||||
|---|---|---|---|---|---|---|
| Date | Time | HomeTeam | WinningTeam | |||
| April 1 2019 | 10:00 PM | PHO | PHO | 453 | 453 | 453 |
| 7:00 PM | IND | IND | 433 | 433 | 433 | |
| 7:30 PM | BOS | BOS | 455 | 455 | 455 | |
| BRK | MIL | 541 | 541 | 541 | ||
| NYK | NYK | 433 | 433 | 433 | ||
| ... | ... | ... | ... | ... | ... | ... |
| October 31 2018 | 10:30 PM | PHO | SAS | 451 | 451 | 451 |
| 7:30 PM | BRK | BRK | 571 | 571 | 571 | |
| 8:00 PM | CHI | DEN | 488 | 488 | 488 | |
| MIN | MIN | 494 | 494 | 494 | ||
| NYK | IND | 433 | 433 | 433 |
1312 rows × 3 columns
games = [x[0] for x in games_groupby ]
home_wins = [int(game[2]==game[3]) for game in games]
home_wins[:10]
[1, 1, 1, 0, 1, 1, 0, 1, 1, 1]
prior_home_win = sum(home_wins)/len(home_wins)
print(prior_home_win)
0.5907012195121951
games_groupby_zip = games_groupby.apply(lambda x: list(zip([t for t in x['time_left']], [p for p in x['home_pt_diff']])))
t_p_win = list(zip(games_groupby_zip, home_wins))
t_p_win[0]
([(2880, 0),
(2861, 0),
(2855, 0),
(2852, 0),
(2838, 0),
(2835, 0),
(2818, 0),
(2816, 0),
(2803, 2),
(2776, 2),
(2774, 2),
(2768, 2),
(2767, 2),
(2760, 2),
(2752, 2),
(2749, 4),
(2734, 4),
(2731, 4),
(2730, 2),
(2727, 2),
(2727, 2),
(2710, 0),
(2694, 3),
(2682, 3),
(2680, 3),
(2665, 3),
(2665, 3),
(2657, 3),
(2657, 3),
(2644, 3),
(2641, 3),
(2623, 3),
(2621, 3),
(2612, 3),
(2597, 1),
(2579, 4),
(2559, 4),
(2556, 4),
(2550, 4),
(2548, 4),
(2541, 4),
(2541, 4),
(2541, 4),
(2532, 4),
(2532, 4),
(2517, 7),
(2517, 7),
(2517, 8),
(2495, 6),
(2472, 8),
(2472, 8),
(2472, 8),
(2472, 8),
(2472, 9),
(2458, 9),
(2455, 9),
(2455, 7),
(2455, 7),
(2455, 7),
(2455, 7),
(2448, 7),
(2432, 7),
(2430, 7),
(2414, 5),
(2396, 8),
(2374, 8),
(2372, 8),
(2368, 8),
(2368, 8),
(2368, 8),
(2355, 6),
(2343, 6),
(2322, 4),
(2305, 4),
(2303, 4),
(2296, 4),
(2296, 4),
(2296, 4),
(2296, 3),
(2296, 2),
(2296, 2),
(2280, 2),
(2272, 2),
(2272, 2),
(2272, 2),
(2272, 2),
(2270, 2),
(2258, 2),
(2256, 2),
(2254, 2),
(2250, 2),
(2244, 2),
(2243, 2),
(2241, 0),
(2234, 0),
(2234, 0),
(2223, -2),
(2223, -2),
(2223, -3),
(2211, -3),
(2210, -3),
(2205, 0),
(2197, 0),
(2195, 0),
(2192, 2),
(2173, 2),
(2172, 2),
(2172, 2),
(2172, 3),
(2172, 3),
(2172, 3),
(2172, 4),
(2165, 4),
(2165, 4),
(2165, 4),
(2160, 7),
(2160, 7),
(2160, 8),
(2160, 8),
(2148, 10),
(2133, 10),
(2131, 10),
(2118, 12),
(2103, 10),
(2078, 10),
(2075, 10),
(2068, 10),
(2065, 10),
(2060, 10),
(2059, 10),
(2048, 10),
(2046, 10),
(2040, 12),
(2018, 12),
(2017, 12),
(2014, 14),
(2014, 14),
(2014, 14),
(2012, 14),
(2004, 14),
(2003, 14),
(1997, 14),
(1994, 14),
(1985, 14),
(1985, 15),
(1985, 15),
(1985, 16),
(1973, 16),
(1963, 13),
(1945, 13),
(1935, 13),
(1934, 13),
(1926, 13),
(1923, 13),
(1916, 13),
(1916, 13),
(1916, 13),
(1916, 14),
(1906, 11),
(1888, 14),
(1878, 14),
(1878, 14),
(1878, 14),
(1878, 14),
(1866, 17),
(1864, 17),
(1864, 17),
(1847, 15),
(1830, 17),
(1808, 17),
(1808, 17),
(1799, 15),
(1787, 17),
(1763, 17),
(1763, 16),
(1763, 16),
(1763, 15),
(1748, 15),
(1745, 15),
(1745, 15),
(1737, 15),
(1733, 15),
(1728, 18),
(1728, 18),
(1728, 19),
(1706, 17),
(1684, 17),
(1682, 17),
(1672, 15),
(1672, 15),
(1672, 14),
(1672, 14),
(1672, 14),
(1672, 14),
(1665, 14),
(1665, 15),
(1665, 16),
(1653, 14),
(1653, 14),
(1653, 14),
(1651, 14),
(1635, 16),
(1617, 14),
(1598, 17),
(1583, 17),
(1582, 17),
(1581, 17),
(1581, 16),
(1581, 15),
(1566, 17),
(1545, 15),
(1531, 15),
(1529, 15),
(1518, 15),
(1516, 15),
(1511, 17),
(1498, 17),
(1495, 17),
(1488, 17),
(1487, 17),
(1482, 17),
(1482, 18),
(1482, 18),
(1482, 18),
(1482, 18),
(1482, 19),
(1463, 17),
(1441, 19),
(1441, 19),
(1441, 19),
(1440, 19),
(1426, 19),
(1417, 21),
(1396, 21),
(1395, 21),
(1395, 21),
(1395, 22),
(1380, 22),
(1362, 22),
(1356, 22),
(1344, 22),
(1341, 22),
(1333, 20),
(1320, 20),
(1317, 20),
(1307, 18),
(1297, 18),
(1284, 18),
(1282, 18),
(1280, 18),
(1280, 18),
(1280, 18),
(1280, 18),
(1280, 17),
(1262, 17),
(1260, 17),
(1260, 17),
(1260, 17),
(1246, 14),
(1244, 14),
(1244, 14),
(1233, 16),
(1214, 14),
(1214, 14),
(1214, 14),
(1212, 14),
(1195, 16),
(1180, 16),
(1178, 16),
(1172, 19),
(1161, 16),
(1148, 16),
(1146, 16),
(1132, 16),
(1131, 16),
(1124, 16),
(1119, 16),
(1116, 16),
(1113, 18),
(1112, 18),
(1112, 18),
(1094, 16),
(1068, 16),
(1067, 16),
(1066, 16),
(1054, 16),
(1049, 18),
(1032, 16),
(1014, 16),
(1012, 16),
(1007, 16),
(1007, 16),
(999, 14),
(988, 16),
(975, 14),
(970, 14),
(970, 14),
(966, 14),
(965, 14),
(952, 14),
(951, 14),
(948, 14),
(948, 14),
(948, 14),
(948, 14),
(948, 14),
(948, 13),
(934, 13),
(930, 13),
(930, 13),
(928, 13),
(925, 13),
(923, 13),
(922, 11),
(922, 11),
(915, 11),
(912, 11),
(903, 11),
(900, 11),
(895, 11),
(887, 11),
(884, 11),
(875, 9),
(857, 11),
(837, 11),
(837, 10),
(837, 9),
(830, 9),
(817, 9),
(814, 9),
(806, 9),
(803, 9),
(803, 7),
(797, 7),
(795, 7),
(792, 7),
(791, 7),
(790, 7),
(773, 7),
(771, 7),
(766, 7),
(764, 7),
(759, 9),
(746, 7),
(727, 7),
(722, 7),
(722, 7),
(720, 7),
(703, 5),
(683, 5),
(682, 5),
(682, 5),
(673, 7),
(646, 7),
(643, 7),
(631, 9),
(631, 9),
(631, 9),
(631, 9),
(629, 9),
(621, 9),
(619, 9),
(612, 11),
(612, 11),
(612, 11),
(612, 11),
(612, 12),
(592, 12),
(591, 12),
(587, 15),
(570, 15),
(555, 15),
(551, 15),
(541, 15),
(541, 14),
(541, 13),
(524, 15),
(513, 15),
(511, 15),
(507, 17),
(507, 17),
(496, 14),
(478, 14),
(477, 14),
(474, 16),
(445, 16),
(445, 16),
(433, 16),
(433, 16),
(433, 16),
(433, 16),
(433, 16),
(427, 16),
(407, 16),
(395, 16),
(393, 16),
(386, 16),
(384, 16),
(373, 16),
(372, 16),
(370, 14),
(351, 14),
(349, 14),
(342, 11),
(340, 11),
(340, 11),
(340, 11),
(324, 13),
(310, 13),
(309, 13),
(308, 11),
(291, 11),
(288, 11),
(273, 11),
(272, 11),
(271, 9),
(248, 9),
(246, 9),
(226, 9),
(224, 9),
(219, 9),
(216, 9),
(212, 6),
(196, 8),
(174, 8),
(170, 8),
(168, 8),
(168, 9),
(168, 10),
(158, 10),
(145, 12),
(145, 12),
(145, 12),
(122, 12),
(120, 12),
(117, 12),
(116, 12),
(114, 9),
(98, 11),
(85, 9),
(85, 9),
(85, 8),
(67, 10),
(58, 10),
(56, 10),
(36, 13),
(36, 13),
(31, 13),
(28, 13),
(28, 11),
(21, 11),
(21, 9),
(0, 9)],
1)
def probability(t,p, t_p_win):
total_games = 0
home_wins = 0
games = []
for pbp, home_win in t_p_win:
previous_play = (2880,0)
occurred=0
for play in pbp:
if (p==previous_play[1] or p==play[1]) and (t<=previous_play[0] and t>=play[0]):
occurred = 1
games.append((pbp, home_win))
previous_play = play
if occurred == 1:
total_games+=1
home_wins+=home_win
return (home_wins, total_games, games, home_wins/total_games*100)
w,t,games,p = probability(0, -2, t_p_win)
print(w,t,p)
40 44 90.9090909090909
Interestingly even with zero seconds left and a lead for the home team there is a possibility for a loss. This is because the zero seconds left is not precise, there could be 0.3 seconds left for example. The below game is an example.
print(games[0])
([(2880, 0), (2860, -2), (2849, -2), (2845, -2), (2833, -5), (2820, -3), (2802, -3), (2799, -3), (2796, -3), (2792, -3), (2782, -3), (2779, -3), (2770, -3), (2763, -3), (2758, -6), (2746, -6), (2738, -4), (2727, -4), (2723, -4), (2716, -4), (2713, -4), (2698, -6), (2685, -3), (2675, -3), (2675, -4), (2675, -5), (2670, -5), (2661, -2), (2648, -2), (2645, -2), (2634, -2), (2630, -2), (2627, 0), (2608, 0), (2605, 0), (2601, 0), (2598, 0), (2587, 0), (2583, 0), (2575, 0), (2572, 0), (2570, -2), (2548, 1), (2530, -1), (2521, -1), (2521, -1), (2521, -1), (2521, -1), (2511, -1), (2507, -1), (2507, -1), (2507, -1), (2507, -1), (2507, -1), (2507, -1), (2507, 0), (2507, 1), (2496, -1), (2483, -1), (2480, -1), (2478, 2), (2465, 2), (2462, 2), (2452, 2), (2448, 2), (2438, -1), (2424, -1), (2424, 0), (2424, 0), (2424, 0), (2424, 0), (2424, 0), (2420, 0), (2404, 0), (2404, -1), (2404, -1), (2404, -1), (2404, -1), (2404, -2), (2391, -2), (2391, -2), (2385, -2), (2382, -2), (2381, -2), (2379, -4), (2370, -4), (2367, -4), (2367, -4), (2367, -3), (2367, -3), (2367, -2), (2356, -2), (2351, -4), (2331, -4), (2328, -4), (2309, -4), (2306, -4), (2306, -4), (2306, -4), (2306, -4), (2306, -4), (2306, -5), (2306, -6), (2294, -6), (2294, -5), (2290, -5), (2287, -5), (2275, -5), (2273, -5), (2272, -7), (2265, -7), (2265, -7), (2265, -7), (2265, -7), (2265, -8), (2251, -8), (2250, -8), (2247, -6), (2230, -8), (2215, -8), (2215, -7), (2215, -7), (2215, -6), (2190, -6), (2186, -6), (2167, -6), (2163, -6), (2161, -6), (2161, -6), (2161, -6), (2161, -7), (2160, -7), (2160, -7), (2160, -7), (2147, -7), (2143, -9), (2130, -9), (2130, -8), (2130, -7), (2124, -7), (2117, -7), (2114, -7), (2106, -5), (2092, -5), (2081, -5), (2076, -5), (2076, -7), (2072, -5), (2057, -8), (2039, -8), (2037, -8), (2035, -6), (2027, -8), (2014, -8), (2011, -8), (2007, -8), (2003, -8), (2001, -8), (2001, -7), (2001, -7), (2001, -7), (2001, -6), (1994, -6), (1994, -7), (1994, -7), (1994, -8), (1986, -8), (1976, -8), (1972, -8), (1972, -6), (1960, -9), (1937, -7), (1926, -7), (1922, -7), (1920, -7), (1914, -10), (1895, -10), (1895, -10), (1895, -10), (1895, -10), (1888, -8), (1888, -8), (1888, -7), (1877, -7), (1869, -7), (1867, -7), (1859, -7), (1856, -7), (1855, -7), (1854, -7), (1853, -7), (1851, -7), (1850, -7), (1849, -7), (1845, -9), (1845, -9), (1845, -9), (1845, -10), (1835, -10), (1835, -10), (1835, -10), (1835, -10), (1835, -10), (1835, -9), (1822, -9), (1820, -9), (1812, -7), (1800, -9), (1800, -9), (1800, -10), (1792, -7), (1779, -7), (1779, -7), (1779, -7), (1779, -7), (1779, -6), (1779, -5), (1770, -5), (1765, -5), (1757, -2), (1736, -2), (1736, -2), (1730, -2), (1727, -2), (1718, 0), (1718, 0), (1718, 1), (1701, 1), (1701, 1), (1686, 1), (1684, 1), (1679, -1), (1665, 1), (1658, 1), (1658, 0), (1658, -1), (1643, -1), (1643, -1), (1623, -1), (1614, 1), (1603, 1), (1603, 1), (1603, 1), (1603, 1), (1603, 1), (1591, -2), (1572, -2), (1569, -2), (1556, -2), (1554, -2), (1545, -2), (1539, -2), (1539, -2), (1538, -2), (1537, -2), (1533, -2), (1526, -2), (1521, -2), (1521, -2), (1507, -2), (1505, -2), (1505, -2), (1505, -3), (1505, -4), (1491, -4), (1489, -4), (1489, -2), (1473, -4), (1469, -1), (1467, -1), (1467, -2), (1467, -3), (1451, -3), (1451, -3), (1451, -3), (1451, -2), (1443, -2), (1443, -3), (1443, -4), (1440, -4), (1440, -4), (1440, -4), (1427, -1), (1415, -1), (1412, -1), (1405, -1), (1402, -1), (1395, -1), (1393, -1), (1390, -1), (1386, -1), (1369, -1), (1366, -1), (1360, -1), (1356, -1), (1354, -1), (1353, -3), (1353, -3), (1353, -3), (1353, -3), (1350, -3), (1328, -3), (1327, -5), (1327, -5), (1312, -5), (1310, -5), (1310, -6), (1310, -6), (1308, -6), (1308, -6), (1308, -7), (1308, -8), (1297, -8), (1297, -7), (1297, -7), (1294, -7), (1282, -7), (1281, -7), (1280, -9), (1268, -9), (1268, -8), (1268, -7), (1253, -9), (1237, -6), (1219, -6), (1217, -6), (1212, -6), (1208, -6), (1205, -6), (1201, -6), (1198, -6), (1189, -6), (1189, -6), (1180, -6), (1174, -3), (1173, -3), (1173, -3), (1162, -5), (1162, -5), (1146, -3), (1121, -6), (1106, -6), (1098, -8), (1098, -8), (1098, -8), (1096, -8), (1089, -8), (1088, -8), (1088, -8), (1075, -6), (1058, -6), (1056, -6), (1051, -6), (1051, -5), (1051, -5), (1051, -5), (1051, -5), (1051, -4), (1033, -7), (1017, -7), (1017, -6), (1017, -6), (1017, -6), (1017, -5), (1003, -5), (1001, -5), (1000, -5), (999, -5), (998, -5), (998, -6), (998, -7), (998, -7), (991, -7), (991, -7), (991, -7), (991, -6), (991, -6), (988, -6), (968, -6), (964, -6), (960, -4), (953, -4), (952, -4), (952, -4), (952, -4), (952, -4), (944, -4), (941, -4), (935, -4), (935, -5), (935, -5), (935, -6), (920, -3), (898, -3), (894, -5), (894, -5), (885, -5), (882, -5), (873, -8), (849, -6), (833, -6), (833, -6), (833, -6), (833, -7), (815, -7), (810, -7), (810, -7), (809, -7), (805, -7), (802, -7), (798, -7), (797, -7), (797, -7), (797, -7), (797, -7), (797, -7), (797, -6), (788, -9), (776, -9), (773, -9), (759, -9), (753, -9), (752, -9), (748, -9), (747, -7), (730, -9), (722, -6), (720, -6), (702, -8), (683, -8), (682, -10), (682, -10), (672, -10), (670, -10), (670, -10), (654, -10), (650, -10), (646, -7), (620, -7), (620, -8), (620, -9), (606, -9), (594, -11), (593, -11), (593, -11), (578, -11), (578, -11), (578, -11), (578, -10), (578, -10), (575, -10), (564, -10), (560, -10), (554, -10), (552, -10), (544, -12), (538, -10), (523, -10), (519, -10), (507, -10), (503, -10), (501, -10), (493, -10), (493, -10), (493, -10), (493, -10), (479, -8), (456, -10), (438, -7), (424, -7), (421, -7), (415, -5), (414, -5), (414, -5), (414, -5), (414, -5), (405, -5), (401, -5), (390, -5), (379, -5), (374, -5), (374, -5), (374, -5), (371, -5), (368, -5), (354, -5), (351, -5), (341, -2), (338, -2), (338, -2), (338, -2), (329, -2), (324, -2), (323, -2), (321, -2), (318, -5), (304, -5), (298, -5), (291, -5), (287, -5), (283, -5), (283, -4), (283, -3), (267, -3), (264, -3), (255, -3), (253, -3), (251, -1), (251, -1), (251, -1), (251, 0), (239, -2), (226, 1), (203, 1), (200, 1), (200, 1), (200, 1), (188, 1), (185, 1), (180, 1), (180, 1), (175, 1), (167, -1), (145, -1), (143, -1), (128, -1), (124, -1), (113, -1), (110, -1), (99, -1), (96, -1), (81, -1), (75, -1), (69, 1), (69, 1), (61, -1), (48, 1), (36, -1), (29, -1), (29, -1), (29, -1), (29, -1), (29, -1), (7, -1), (3, -1), (3, -1), (3, -1), (3, -1), (3, -1), (2, 2), (1, 2), (1, 2), (1, 2), (0, 2), (0, 1), (0, 0), (0, 0), (0, 0), (0, -1), (0, -1)], 0)
# How important is a 2 point lead for the home team
time = reversed(range(0,2881,15))
prob = [probability(t,2,t_p_win)[3] for t in time]
prob
[60.46511627906976,
60.55776892430279,
62.94277929155313,
65.43909348441926,
62.71186440677966,
61.59695817490495,
63.75545851528385,
64.39024390243902,
64.03940886699507,
63.63636363636363,
62.5,
59.47712418300654,
57.85714285714286,
59.541984732824424,
65.54054054054053,
68.48484848484848,
63.1578947368421,
65.06849315068493,
58.108108108108105,
56.9620253164557,
52.41379310344828,
52.41935483870967,
49.166666666666664,
55.00000000000001,
60.0,
60.447761194029844,
60.97560975609756,
63.565891472868216,
62.30769230769231,
59.154929577464785,
60.15625,
63.2,
62.39316239316239,
67.0,
63.30275229357798,
63.06306306306306,
62.264150943396224,
50.505050505050505,
50.526315789473685,
56.52173913043478,
58.82352941176471,
58.76288659793815,
64.48598130841121,
66.30434782608695,
56.470588235294116,
58.0246913580247,
65.4320987654321,
60.0,
55.55555555555556,
57.30337078651685,
62.5,
61.111111111111114,
58.88888888888889,
59.49367088607595,
62.33766233766234,
64.63414634146342,
59.45945945945946,
59.42028985507246,
57.14285714285714,
64.58333333333334,
62.88659793814433,
58.139534883720934,
57.14285714285714,
60.97560975609756,
61.627906976744185,
58.46153846153847,
68.18181818181817,
67.03296703296702,
63.1578947368421,
64.61538461538461,
60.810810810810814,
64.0,
63.1578947368421,
65.33333333333333,
68.65671641791045,
68.75,
64.17910447761194,
66.66666666666666,
59.67741935483871,
66.10169491525424,
63.63636363636363,
56.25,
57.14285714285714,
62.19512195121951,
64.28571428571429,
67.12328767123287,
68.11594202898551,
60.0,
56.52173913043478,
60.3448275862069,
57.8125,
58.666666666666664,
55.55555555555556,
60.810810810810814,
60.273972602739725,
57.534246575342465,
56.75675675675676,
57.971014492753625,
65.0,
63.23529411764706,
67.16417910447761,
68.85245901639344,
66.66666666666666,
71.01449275362319,
67.1875,
65.15151515151516,
67.16417910447761,
66.66666666666666,
64.0625,
64.70588235294117,
75.38461538461539,
71.875,
70.0,
63.1578947368421,
63.63636363636363,
62.96296296296296,
62.5,
59.67741935483871,
69.81132075471697,
68.75,
62.903225806451616,
64.17910447761194,
60.0,
64.28571428571429,
63.49206349206349,
64.7887323943662,
65.15151515151516,
68.25396825396825,
69.23076923076923,
72.3076923076923,
72.3076923076923,
73.33333333333333,
70.6896551724138,
66.07142857142857,
66.15384615384615,
68.33333333333333,
73.21428571428571,
76.0,
72.54901960784314,
66.66666666666666,
68.08510638297872,
65.9090909090909,
64.44444444444444,
67.3913043478261,
63.76811594202898,
70.17543859649122,
73.58490566037736,
78.18181818181819,
75.92592592592592,
66.0377358490566,
68.42105263157895,
69.23076923076923,
73.58490566037736,
71.42857142857143,
67.24137931034483,
63.934426229508205,
64.58333333333334,
73.68421052631578,
66.66666666666666,
61.702127659574465,
58.620689655172406,
60.0,
67.27272727272727,
76.47058823529412,
75.51020408163265,
75.51020408163265,
65.95744680851064,
67.24137931034483,
62.06896551724138,
64.91228070175438,
70.17543859649122,
62.903225806451616,
65.0,
69.81132075471697,
66.66666666666666,
70.83333333333334,
74.50980392156863,
76.92307692307693,
71.1864406779661,
63.793103448275865,
59.67741935483871,
65.57377049180327,
62.96296296296296,
64.0,
71.11111111111111,
72.3404255319149,
62.5,
68.29268292682927,
66.66666666666666,
68.18181818181817,
85.41666666666666,
92.0,
90.9090909090909]
time = range(0,2881,15)
plt.plot([t for t in time], prob)
[<matplotlib.lines.Line2D at 0x7f22371edd30>]
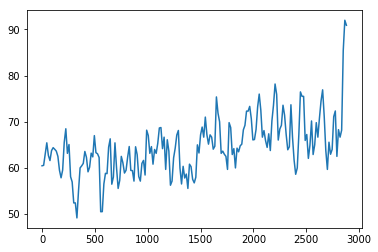
Above graph of win percentages is not very smooth, would be interesting to consider ways to smooth this graph out. Applying other ML algorithms to this could help with this since ML algorithms assume a smooth underlying probability function.