Implementing k-Nearest Neighbors
This is an implementation of k_Nearest neighbors using only the most basic python libraries. This algorithm takes make predictions by looking at a set of data points that is most similar, called neighbors, and looking at a number of them (k is the variable in the algorithm that specifies the number of neighbors we will look at).
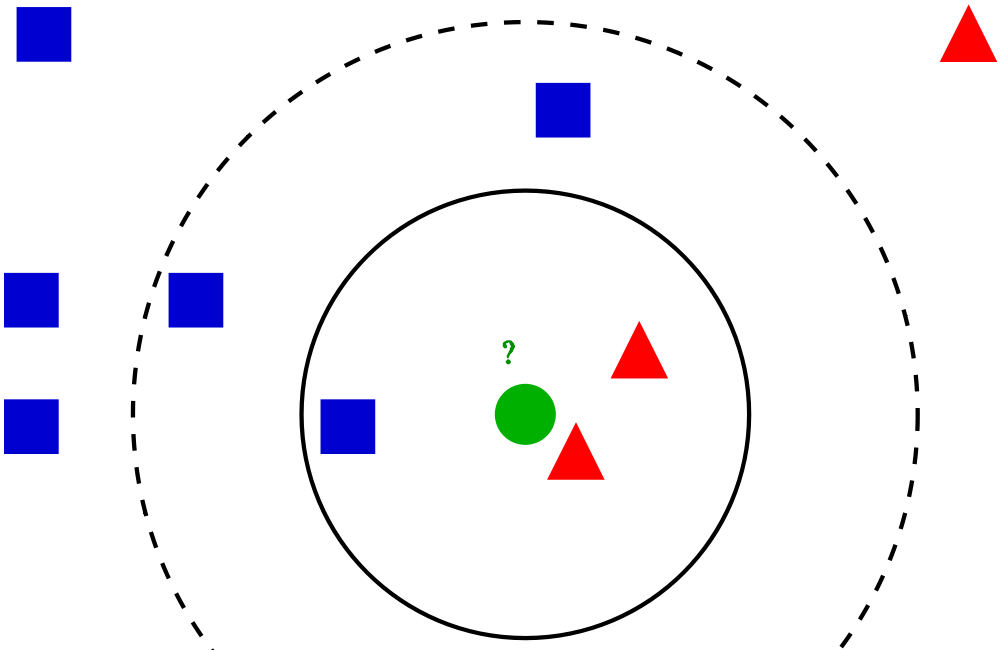
k-Nearest neighbors is a relatively simple algorithm that is supervised (thus attempts to predict a target variable). But k-Nearest neighbors does not require a training period and it is not parameterized, meaning we don’t need to define the training features ahead of time.
We will test this against the popular Iris Dataset
In addition to the above benefits for this algorithm, it is also sometimes used for simple recommendation engines by returning the neighbors for a particular instance. One major downside of the algorithm is that it is computationally expensive.
Thanks to machinelearningmastery.com for this walkthrough: https://machinelearningmastery.com/tutorial-to-implement-k-nearest-neighbors-in-python-from-scratch/
Import Libraries
from csv import reader
from math import sqrt
from random import seed
from random import randrange
from copy import deepcopy
from matplotlib import pyplot as plt
Create k-Nearest Neighbors prediction
# assume that the last column is the target variable
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)-1):
distance+=(row1[i] - row2[i])**2
return sqrt(distance)
def get_k_neighbors(train, instance, k):
distances = []
for row in train:
dist = euclidean_distance(row, instance)
distances.append((row, dist))
distances.sort(key=lambda tup: tup[1])
neighbors = []
for i in range(k):
neighbors.append(distances[i][0])
return neighbors
def predict_k_neighbors(train, instance, k):
neighbors = get_k_neighbors(train, instance, k)
output_values = [row[-1] for row in neighbors]
prediction = max(set(output_values), key=output_values.count)
return prediction
def k_nearest_neighbors(train, to_predict, k):
predictions = []
col_mins = []
col_maxs = []
for i in range(len(train[0])-1):
values_in_col = [row[i] for row in train]
col_min = min(values_in_col)
col_max = max(values_in_col)
col_mins.append(col_min)
col_maxs.append(col_max)
train_norm = deepcopy(train)
for row in train_norm:
for i in range(len(row)-1):
row[i] = (row[i] - col_mins[i])/(col_maxs[i] - col_mins[i])
to_predict_norm = deepcopy(to_predict)
for row in to_predict_norm:
for i in range(len(row)-1):
row[i] = (row[i] - col_mins[i])/(col_maxs[i] - col_mins[i])
output = predict_k_neighbors(train_norm, row, k)
predictions.append(output)
return(predictions)
Test algorithm against Iris Dataset
dataset = []
with open('iris.csv', 'r') as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
for i in range(len(row)-1):
row[i] = float(row[i])
dataset.append(row)
dataset[:5]
[[5.1, 3.5, 1.4, 0.2, 'Iris-setosa'],
[4.9, 3.0, 1.4, 0.2, 'Iris-setosa'],
[4.7, 3.2, 1.3, 0.2, 'Iris-setosa'],
[4.6, 3.1, 1.5, 0.2, 'Iris-setosa'],
[5.0, 3.6, 1.4, 0.2, 'Iris-setosa']]
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = []
for validation_fold in folds:
train_set = [row for row in dataset if not(row in validation_fold)]
predicted = algorithm(train_set, validation_fold, *args)
actual = [row[-1] for row in validation_fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
def cross_validation_split(dataset, n_folds):
dataset_folds = []
dataset_copy = dataset.copy()
fold_size = int(len(dataset_copy)/n_folds)
for _ in range(n_folds):
fold = []
while len(fold) < fold_size:
rand_index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(rand_index))
dataset_folds.append(fold)
return dataset_folds
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct+=1
return correct / float(len(actual)) * 100.0
seed(123)
scores = evaluate_algorithm(dataset, k_nearest_neighbors, 5, 5)
print(f'Scores: {scores}')
print(f'Mean Accuracy: {sum(scores)/float(len(scores)):.2f}')
Scores: [96.66666666666667, 96.66666666666667, 90.0, 93.33333333333333, 100.0]
Mean Accuracy: 95.33
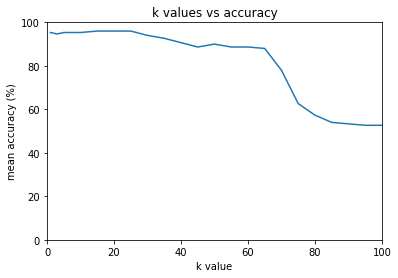
Test various k values
# using cross validation (with 5 folds) to test different k values
k_values = [1,3]
k_values.extend([5*i for i in range(1,21)])
mean_accuracies = {}
for k in k_values:
seed(123)
scores = evaluate_algorithm(dataset, k_nearest_neighbors, 5, k)
mean_accuracies[k] = sum(scores)/float(len(scores))
for k, ma in mean_accuracies.items():
print(f'{k}: {ma:.2f}%')
1: 95.33%
3: 94.67%
5: 95.33%
10: 95.33%
15: 96.00%
20: 96.00%
25: 96.00%
30: 94.00%
35: 92.67%
40: 90.67%
45: 88.67%
50: 90.00%
55: 88.67%
60: 88.67%
65: 88.00%
70: 78.00%
75: 62.67%
80: 57.33%
85: 54.00%
90: 53.33%
95: 52.67%
100: 52.67%
x = [item[0] for item in mean_accuracies.items()]
y = [item[1] for item in mean_accuracies.items()]
plt.figure()
plt.plot(x, y)
plt.xlabel('k value')
plt.ylabel('mean accuracy (%)')
plt.axis([0, 100, 0, 100])
plt.title('k values vs accuracy')
plt.show()